jueves, 29 de noviembre de 2012
lunes, 22 de octubre de 2012
Teselaciones
1) Materiales
1.-Cartulina de colores
2.-Carton piedra
3.-Tempera
4.-Plumòn negro
5.-Scotch
2) Como se hace
1.-Se marcan las figuras (eso depende de la teselacion que hagas).
2.- Se pegan las figuras en una cartulina según corresponda (sin ningún espacio sobrante).
3.-Se marca el contorno con el plumón.
4.-Se pinta el borde con tempera negra.
5.-Cando la tempera si seque, se forra con scotch.
RESAÑA:
Los teselados son los diseños de figuras geométricas que por sí mismas o en combinación cubren una superficie plana sin dejar huecos ni superponerse, o sea, el cubrimiento del plano con figuras yuxtapuestas.
Posteriormente otros grupos demostraron maestría en este tipo de trabajo. Ellos fueron los persas, los moros y los musulmanes.
El grupo matemático de los pitagóricos analizaron tales construcciones y probablemente éstas los haya conducido al famoso teorema que establece que la suma de los ángulos interiores es igual a un ángulo llano.
La palabra teselado proviene de “tessellae”. Así llamaban los romanos a las construcciones y pavimentos de su ciudad.
Los teselados pueden ser regulares o irregulares. Dentro de los regulares existen los semirregulares y demirregulares.
Los regulares se logran a partir de la repetición y traslación de polígonos regulares.
Los demirregulares se logran a partir de la combinación de varios tipos de polígonos regulares pero de modo que no todos los vértices tengan la misma distribución, en cambio, los semirregulares se forman con la combinación de dos o más polígonos regulares pero distribuidos de modo tal que en todos los vértices aparezcan los mismos polígonos y en el mismo orden.
En un teselado plano regular la suma de todos los ángulos que concurren a un vértice es 360º, por ello, los únicos polígonos regulares que cubren completamente una superficie plana son: el triángulo equilátero, el cuadrado y el hexágono.
TORRES DE HANOI
TORRES DE HANOI
1.- M A T E R I A L E S: a) Carton piedra
b) Corta carton
c) Tijeras
d) Tempera
2.- C O M O S E H A C E:
a) Se marcan 5 tomaños distintos de circunferencia en el corton piedra.
b) Se cortan 5 de cada una de las circunferencias hechas.
c) Se hace un orificio en el centro de las mismas circunferencias.
d) Se pegan 5 circunferencias del mismo tamaño.
e) Se pintan todos las circunferencias hechas de cualquier color.
a) Se marcan 5 tomaños distintos de circunferencia en el corton piedra.
b) Se cortan 5 de cada una de las circunferencias hechas.
c) Se hace un orificio en el centro de las mismas circunferencias.
d) Se pegan 5 circunferencias del mismo tamaño.
e) Se pintan todos las circunferencias hechas de cualquier color.
3.- H I S T O R I A: Se cuenta que un templo de Benarés (Uttar Pradesh, India), se encontraba una cúpula que señalaba el centro del mundo. Allí estaba una bandeja sobre la cual existían tres agujas de diamante. En una mañana lluviosa, un rey mandó a poner 64 discos de oro, siendo ordenados por tamaño: el mayor en la base de la bandeja y el menor arriba de todos los discos.Tras la colocación, los sacerdotes del templo intentaron mover los discos entre las agujas, según las leyes que se les habían entregado: "El sacerdote de turno no debe mover más de un disco a la vez, y no puede situar un disco de mayor diámetro encima de otro de menor diámetro". Hoy no existe tal templo, pero el juego aún perduró en el tiempo.
El mínimo número de movimientos son 8 y se debe buscar la diferencia que se necesita para resolver este problema es de 2-1. Si los monjes hicieran un movimiento por segundo, los 64 discos estarían en la tercera varilla en algo menos de 585 mil millones de años. Como comparación para ver la magnitud de esta cifra, la Tierra tiene como 5 mil millones de años, y el Universo entre 15 y 20 mil millones de años de antigüedad, sólo una pequeña fracción de esa cifra.
4.- D E S C R I P C I O N: El juego, en su forma más tradicional, consiste en tres varillas verticales. En una de las varillas se apila un número indeterminado de discos (elaborados de carton piedra) que determinará la complejidad de la solución, por regla general se consideran 5 discos. Los discos se apilan sobre una varilla en tamaño decreciente. No hay dos discos iguales, y todos ellos están apilados de mayor a menor radio en una de las varillas, quedando las otras dos varillas vacantes. El juego consiste en pasar todos los discos de la varilla ocupada (es decir la que posee la torre) a una de las otras varillas vacantes. Para realizar este objetivo, es necesario seguir tres simples reglas: a) Sólo se puede mover un disco cada vez.
b) Un disco de mayor tamaño no puede descansar sobre uno más pequeño que él mismo.
c)Sólo puedes desplazar el disco que se encuentre arriba en cada varilla.
Existen diversas formas de realizar la solución final, todas ellas siguiendo estrategias diversas.
Usa este enlace para jugar:
http://www.pequejuegos.com/juego-la-torre-de-hanoi.html
5.- I M A G E N E S:
Cubo Soma
1.- Materiales:
2.- ¿Como se hace?
3.- Historia:
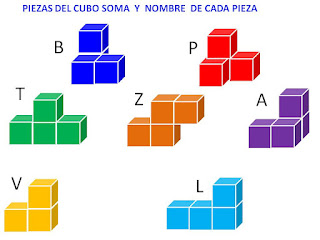
4.- Dibujos de las piezas:
- Madera
- Tempera
- Lija
- Cola fria
- Sierra
- Pincel
2.- ¿Como se hace?
- Se marca la madera
- Cortar la madera
- Se lija la madera
- Se pega para construir las formas (figuras)
- Una vez ya formada, se pinta
- Cuando ya este seco... ¡A Jugar!
El cubo Soma es un rompecabezas geométrico, con siete piezas formadas con cubos que hay que unir para consegir un cubo mayor.
Fue creado por Piet Hein en el año 1936. Se dice que durante una conferencia de Heisenberg Hein empezó a pensar en los distintos policubos que se podían obtener uniendo varios cubos del mismo tamaño, y comprobó que todos los policubos irregulares formados por cuatro o menos cubos sumaban un total de 27 cubos, y podían unirse en un cubo mayor con tres cubos de arista.
Posteriormente, el matemático John Conway comprobó que había 240 formas distintas de resolver el problema principal.
Con las piezas del cubo Soma se pueden crear otras formas, con diseños geométricos más o menos interesantes o incluso diseños figurativos. Hay recopilaciones con miles de estas figuras.
LAS SIETE FIGURAS DEL SOMA SE PUEDEN IDENTIFICAR CON UN NUMERO O CON UNA LETRA. LOS POLICUBOS DE 4 O MENOS CUBOS QUE NO FIGURAN EN ESTA LISTA SON TODOS REGULARES.
4.- Dibujos de las piezas:
 |
Figuras construidas por alumnas del taller
|
5.- Desmostracion:
En el video se muestra la forma de como se juega.
domingo, 21 de octubre de 2012
Pentominó
RESEÑA
Un Pentominó son poliformas de la clase poliominó que consiste en una figura geométrica compuesta por cinco cuadrados unidos por sus lados. Existen doce pentominós diferentes, que se nombran con diferentes letras del abecedario. Los pentominós obtenidos a partir de otros por simetría axial o por rotación no cuentan como un Pentominó diferente.
Historia
Consiste en una figura geométrica compuesta por cinco cuadrados unidos por sus lados. Existen doce pentominós diferentes, que se nombran con diferentes letras del abecedario. Los pentominós obtenidos a partir de otros por simetría axial o por rotación no cuentan como un Pentominó diferente.
- Regla
- Plumón Negro
- Cartulina de Colores
- Block Blanco
- Scotch
PIEZAS
Como Se hace
- Cuadricular un trozo de cartulina
- Marcar las piezas
- Recortar
- Comenzar a armar las figuras deseadas.
Ejemplo:
martes, 16 de octubre de 2012
BIENVENIDA
En este blog, te presentaremos el trabajo realizado durante el año 2012, de las alumnas pertenecientes al taller "talentosas matemáticas".
Todas las actividades fueron realizadas por las alumnas del 2º Ciclo de enseñanza básica del colegio Santa Clara.
Acontinuación, ellas mismas harán una descripcion general de sus creaciones, la función y objetivo que para ellas significó.
Se respalda además material fotografico y videos.
Suscribirse a:
Comentarios (Atom)